Median
Pasti Anda sudah pernah mendengar istilah median, bukan? Median merupakan nilai tengah dari suatu data yang telah diurutkan terlebih dahulu mulai dari yang terkecil hingga terbesar. Dalam matematika, biasanya Median dilambangkan sebagai Me dan dihitung dengan rumus seperti berikut:

Untuk penerapannya perhatikan contoh soal di bawah ini:
Contoh 1 – Median data ganjil
| 3,2,7,12,10 |
Berapakah nilai median dari data di atas?
Pertama, kita urutkan data di atas terlebih dahulu seperti berikut: 2,3,7,10,12.
Karena data di atas ada 5 (n=5) yang berarti ganjil, maka terapkan rumus median ganjil seperti berikut:
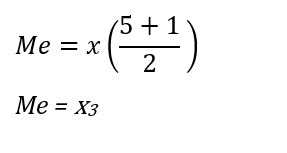
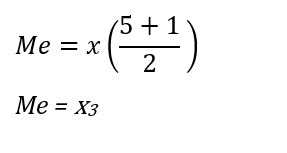
Median menghasilkan x3 yang berarti median data tersebut ada di urutan ke-3. Sehingga dari hasil perhitungan di atas, median dari data di atas adalah 7.
Contoh 2 – Median data genap
|
3,2,7,12,10,3,5,12,15,8
|
Berapakah nilai median dari data di atas?
Sama seperti sebelumnya, kita urutkan dulu datanya menjadi 2,3,3,5,7,8,10,12,12,15
Karena data di atas berjumlah 10 (n=10) yang berarti genap, maka kita terapkan dengan rumus median genap seperti berikut:
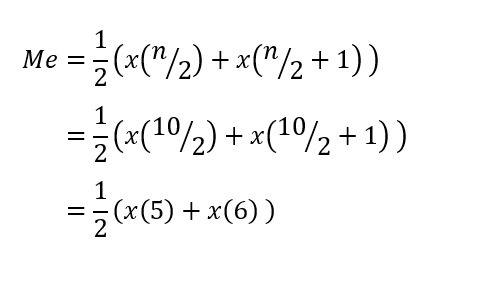
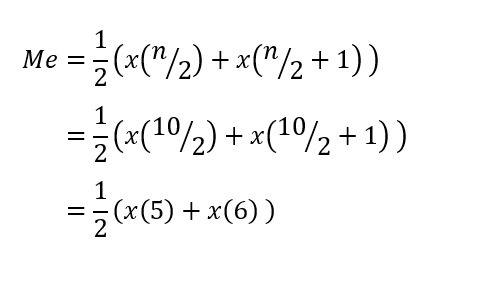
Dari perhitungan di atas didapatkan hasil x5 dan x6 yang berarti kita menjumlahkan elemen data diurutan ke-5 dan urutan ke-6 kemudian dibagi 2.
2,3,3,5,7,8,10,12,12,15
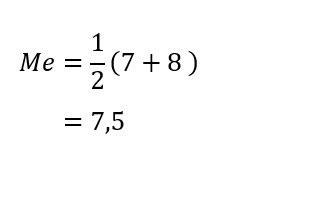
Sehingga nilai median dari data genap di atas adalah 7,5
Modus
Modus merupakan nilai yang sering muncul dari suatu data. Tiada rumus tertentu guna mencari nilai modus karena kita hanya perlu mengamati frekuensi data mana yang sering muncul. Dalam matematika, modus biasanya dilambangkan dengan Mo.
Suatu data bisa jadi memiliki lebih dari satu modus. Apabila sebuah kumpulan data memiliki dua modus, ia disebut bimodal. Sedangkan apabila memiliki lebih dari dua modus ia disebut multimodal. Tetapi ada juga data yang tidak memiliki nilai yang sering muncul sehingga dikatakan data tersebut tidak memiliki modus.
Contoh 1:
Guru matematika mengadakan ulangan di kelas A dan mengambil hasil sampel nilai dari 5 siswanya sebagai berikut.
|
80, 70, 75, 80, 80, 90
|
Tentukan modus dari hasil ulangan matematika dari 5 siswa tersebut!
Jawab:
Untuk menjawab pertanyaan di atas kita hanya memerlukan pengamatan saja tanpa rumus apa pun. Untuk memudahkan kita dalam menemukan modus dari data di atas, kita urutkan terlebih dahulu sehingga hasilnya menjadi seperti di bawah ini.
| 70, 75, 80, 80, 80, 90 |
Sehingga dari hasil pengamatan terlihat bahwa nilai 80 muncul sebanyak 3 kali. Jadi, secara otomatis bisa dikatakan bahwa dari ulangan matematika di atas modusnya adalah 80.
Contoh 2:
Terdapat 10 orang yang sedang mengukur tinggi badannya dan menghasilkan data sebagai berikut.
| 160,153,155,170,165,154,165,160,157,174 |
Sama seperti contoh sebelumnya, kita harus mengurutkannya terlebih dahulu menjadi seperti berikut.
Jawab:
Tentukan modus dari data tinggi badan di atas!
|
153,154,155, 157, 160,160,165,165, 170, 174
|
Dari hasil pengamatan, didapatkan bahwa data yang sering muncul adalah 160 dan 165 yang masing-masing muncul sebanyak dua kali. Jadi dari data tinggi badan di atas terdapat dua modus (bimodal) yaitu 160 dan 165
Range
Dalam kumpulan data yang berbentuk angka pasti ada nilai maksimum dan minimumnya. Range atau bisa disebut dengan rentang data merupakan selisih antara data maksimum dan minimum tersebut. Rumus dari range sebagai berikut.
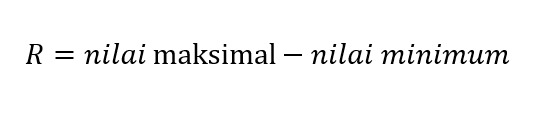
Terdapat kumpulan data dengan nilai sebagai berikut:
| 10, 30, 30, 25, 40, 50, 20 |
Untuk menentukan range dari data di atas, kita dapat mengurutkannya terlebih dahulu mulai dari nilai terkecil sampai terbesar.
| 10, 20, 25, 30, 30, 40, 50 |
Setelah kita mengurutkan data, kita dapat dengan mudah mengetahui bahwa nilai paling kecil adalah 10 dan nilai yang paling besar adalah 50. Sehingga range dari data tersebut bisa mudah dihitung yaitu, 50 – 10 = 40
Kuartil
Apakah Anda familiar dengan kuartil? Kuartil dalam matematika biasanya digambarkan dengan notasi Q. Kuartil merupakan nilai yang membagi data berurutan menjadi 4 bagian yang besarnya sama. Kuartil terdiri dari 3 bagian yaitu, kuartil pertama (Q1), kuartil kedua (Q2), dan kuartil ketiga (Q3). Dalam menghitung nilai kuartil, kita harus memperhatikan jumlah data (n) yang ada.

Gambar di atas merupakan ilustrasi letak kuartil terhadap banyaknya data. Dalam penentuan dan perhitungan kuartil terdapat 4 kondisi dan rumus yang berbeda.
- Banyak data (n) ganjil dan nilai (n+1) habis dibagi 4
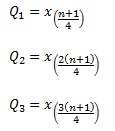
- Banyak data (n) ganjil dan nilai (n+1) tidak habis dibagi 4
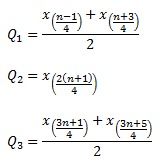
- Banyak data (n) genap dan habis dibagi 4
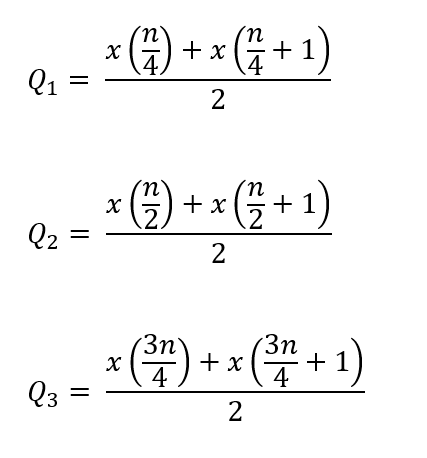
- Banyak data (n) genap dan tidak habis dibagi 4
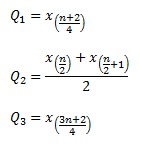
Berikut contoh soal untuk memperjelas tentang kuartil:
Contoh 1:
Hitunglah kuartil dari data panjang jalan tersebut?
| 7, 6, 8, 3, 2 |
Jawab:
Pertama urutkan dulu datanya mulai dari yang terkecil hingga terbesar.
|
2, 3, 6, 7, 8
|
Karena datanya ganjil dan hasil dari (n+1) adalah 6 maka tidak habis dibagi 4. Sehingga kita dapat menggunakan rumus yang kedua seperti berikut:
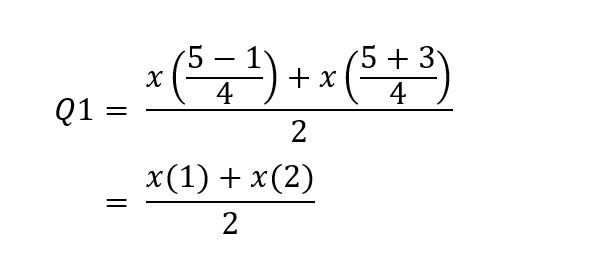
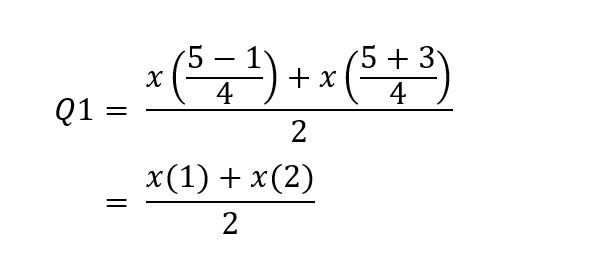
Dari hasil perhitungan di atas diketahui posisi Q1 berada di antara data ke-1 dan ke-2. Untuk menghitung nilainya berarti kita menambahkan x1 dan x2 kemudian dibagi 2 menjadi,
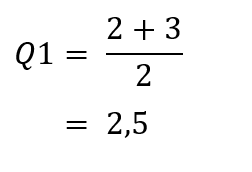
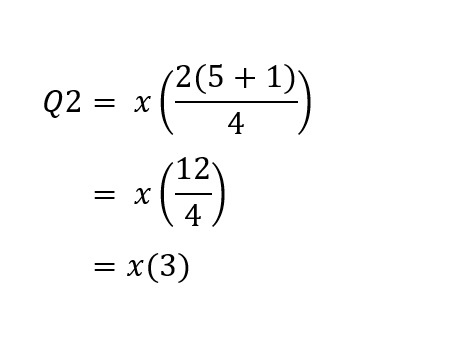
Dari rumus di atas diketahui bahwa letak Q2 berada di data ke-3, sehingga berdasarkan data di atas Q2 = 6.
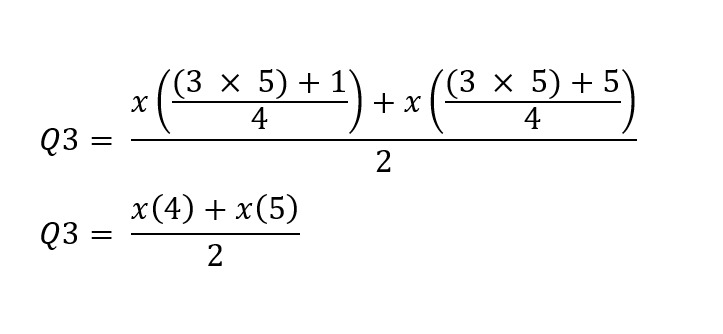
Sama seperti cara sebelumnya, Q3 apabila dilihat dari rumus di atas berarti ada di posisi data ke-4 dan ke-5. Sehingga untuk menghitung nilai dari Q3 menjadi,
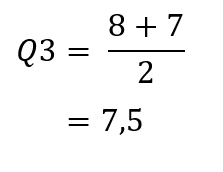
Contoh 2:
Apabila terdapat data berjumlah 430, di manakah posisi masing-masing kuartilnya?
Jawab:
Diketahui bahwa jumlah datanya genap dan tidak habis dibagi 4 berarti kita bisa menggunakan contoh rumus ketiga seperti berikut:
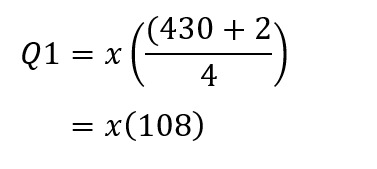
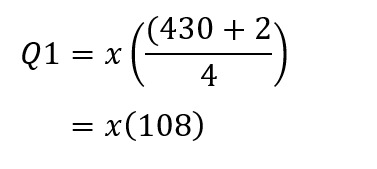
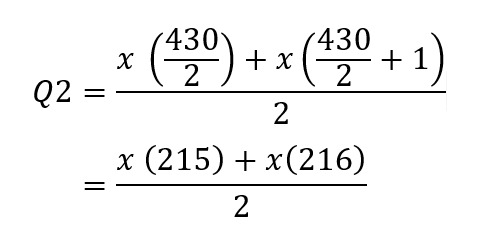
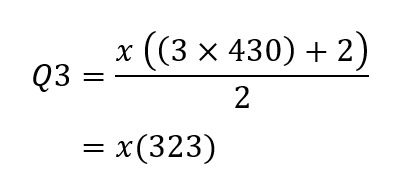
Sehingga dari rumus di atas dapat dilihat bahwa posisi Q1 berada pada data ke-108, Q2 berada di antara data ke-215 dan 216, dan Q3 berada pada data ke-323
Standar Deviasi
Standar deviasi atau disebut dengan simpangan baku adalah ukuran varian atau perbedaan dari nilai sampel terhadap rata-rata suatu data yang sering digunakan dalam statistik. Standar deviasi sendiri juga digunakan untuk mengukur jumlah variasi atau sebaran dari beberapa nilai data. Maka dari itu rumus dari standar deviasi adalah akar kuadrat dari varian. Apabila salah satu nilai dari varian atau standar deviasi diketahui, maka nilai yang lainnya akan dapat mudah ditemukan. Sehingga rumus dari varian adalah sebagai berikut:
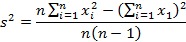
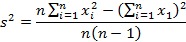
Sedangkan rumus dari varian baku sebagai berikut:
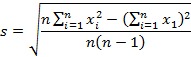
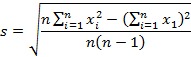
Contoh 1
Untuk lebih memahami tentang standar deviasi, terdapat data tinggi badan siswa seperti di bawah ini.
| 160, 153, 155, 170, 165, 154, 167, 161, 157, 174 |
Dari data di atas diketahui bahwa jumlah data (n = 10) dan jumlah (n – 1) adalah 9. Untuk mempermudah Anda menghitung variannya, mari kita buat dalam bentuk tabel seperti berikut.
|
i
|
Xi
|
Xi2
|
|---|---|---|
|
1
|
160
|
25600
|
|
2
|
153
|
23409
|
|
3
|
155
|
24025
|
|
4
|
170
|
28900
|
|
5
|
165
|
27225
|
|
6
|
154
|
23716
|
|
7
|
167
|
27889
|
|
8
|
161
|
25921
|
|
9
|
157
|
24649
|
|
10
|
174
|
30276
|
|
|
1616
|
261610
|
Jika tabel di atas dituliskan dalam bentuk rumus, seperti ini jadinya:
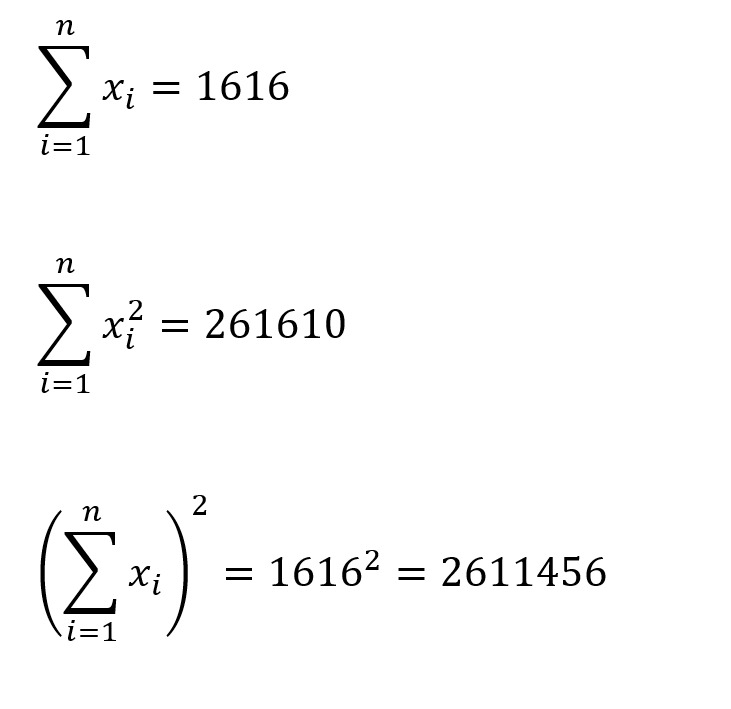
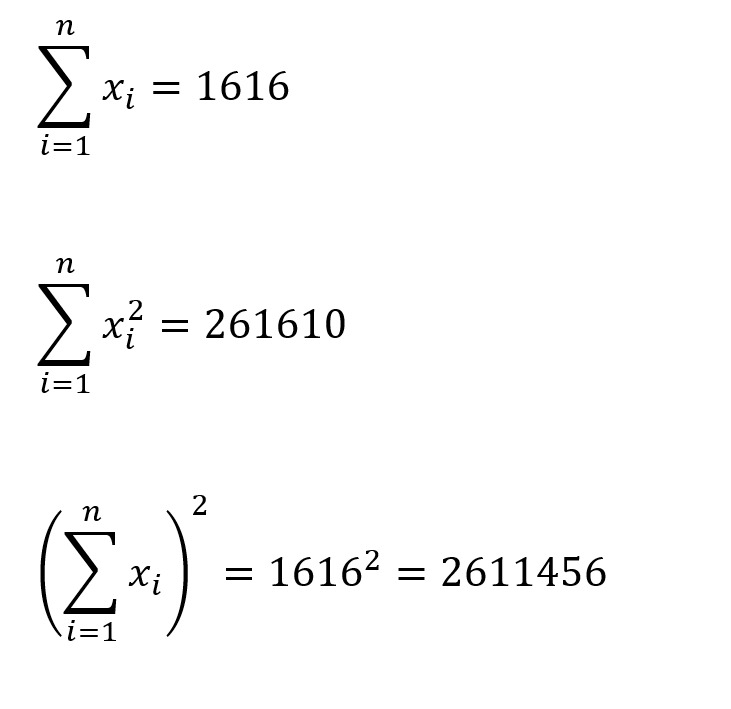
Dari perhitungan yang sudah diketahui dari rumus di atas, apabila angka dimasukkan ke dalam rumus varian. Maka menjadi sebagai berikut:
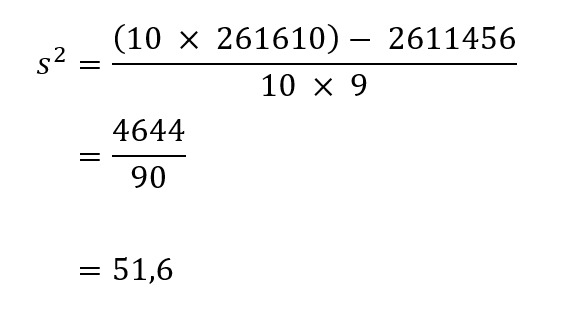
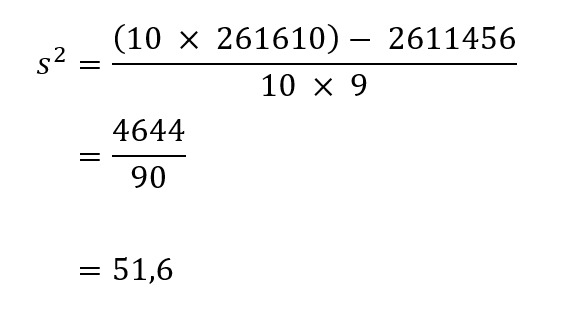
Sehingga kita mendapatkan nilai varian dari data tersebut yaitu 51,6.
Dari nilai varian di atas, kita juga dapat mencari nilai standar deviasi atau simpangan bakunya dengan cara sebagai berikut:
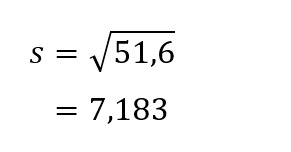
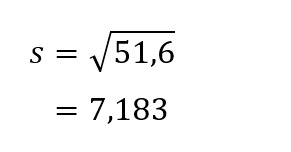
Contoh 2
Seorang guru matematika ingin menguji pemahaman materi dan metode belajar yang tepat bagi siswanya. Ia membagi satu kelas menjadi 2 kelompok siswa yang masing-masing 10 orang. Anggap saja kelompok A dan kelompok B. Kelompok A diberikan waktu belajar sehari sedangkan kelompok B diberikan waktu belajar tiga hari.
Pada hari yang ditentukan setelah kelompok A selesai belajar dalam waktu sehari, guru matematika tersebut mengadakan ulangan harian. Singkat kata, hasil dari ulangannya sebagai berikut:
| Siswa ke- | Nilai |
|---|---|
|
1
|
70
|
|
2
|
65
|
|
3
|
50
|
|
4
|
80
|
|
5
|
75
|
|
6
|
45
|
|
7
|
55
|
|
8
|
75
|
|
9
|
80
|
|
10
|
60
|
Berselang tiga hari kemudian kelompok B melakukan ulangan matematika yang sama seperti kelompok A. Nilai ulangan matematika Kelompok B sebagai berikut:
|
Siswa ke-
|
Nilai
|
|---|---|
|
1
|
65
|
|
2
|
40
|
|
3
|
90
|
|
4
|
55
|
|
5
|
45
|
|
6
|
85
|
|
7
|
55
|
|
8
|
70
|
|
9
|
60
|
|
10
|
75
|
Dari permasalahan di atas, guru matematika tersebut ingin menghitung standar deviasi dari masing-masing kelompok untuk mengukur apakah waktu belajar siswa mempengaruhi hasil ulangan. Bagaimanakah hasilnya?
Jawab:
Pertama kita mulai menghitung dari kelompok A. Sama seperti pada contoh soal sebelumnya, kita tentukan dulu varian sebagai berikut:
|
i
|
x
|
x2
|
|---|---|---|
|
1
|
70
|
4900
|
|
2
|
65
|
4225
|
|
3
|
50
|
2500
|
|
4
|
80
|
6400
|
|
5
|
75
|
5625
|
|
6
|
45
|
2025
|
|
7
|
55
|
3025
|
|
8
|
75
|
5625
|
|
9
|
80
|
6400
|
|
10
|
60
|
3600
|
|
Total
|
655
|
44325
|
Jika tabel di atas dituliskan dalam bentuk rumus, seperti ini jadinya:
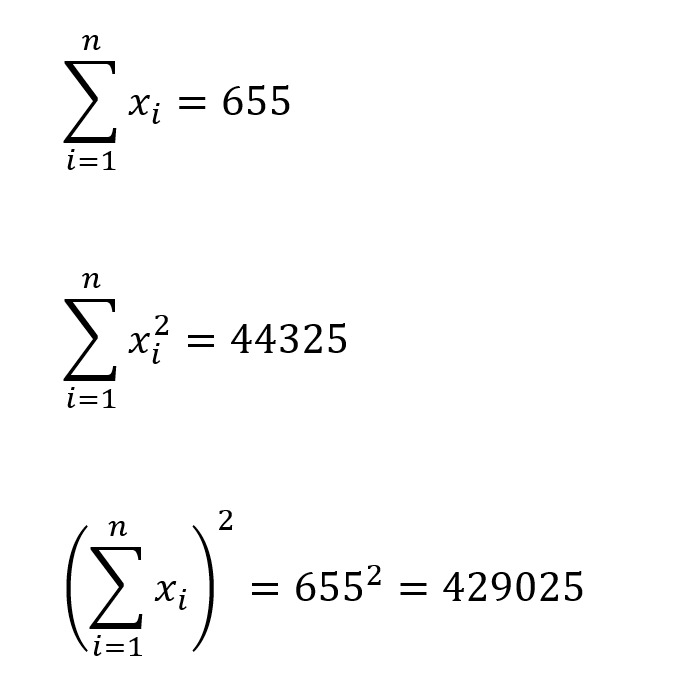
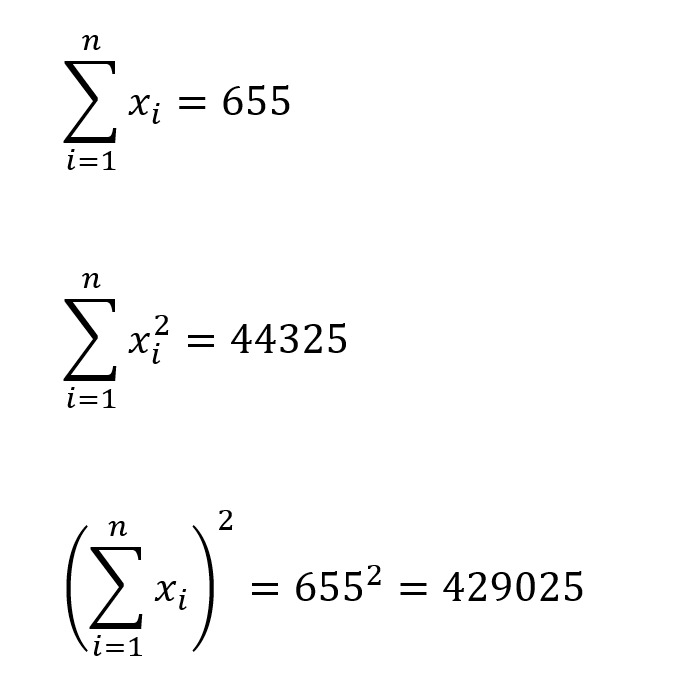
Dari perhitungan yang sudah diketahui dari rumus di atas, apabila angka dimasukkan ke dalam rumus varian. Maka menjadi sebagai berikut:


Sehingga kita mendapatkan nilai varian dari data tersebut yaitu 158,05.
Dari nilai varian di atas, kita juga dapat mencari nilai standar deviasi atau simpangan bakunya dengan cara sebagai berikut:
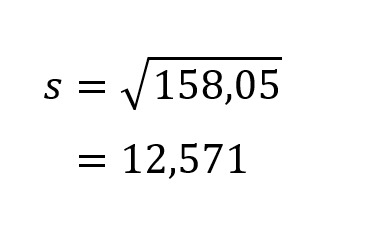
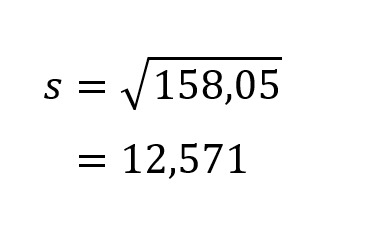
Kita simpan dulu hasilnya perhitungan untuk kelompok A. Selanjutnya kita akan mulai menghitung hasil dari kelompok B.
|
i
|
X
|
X2
|
|---|---|---|
|
1
|
65
|
4225
|
|
2
|
40
|
1600
|
|
3
|
90
|
8100
|
|
4
|
55
|
3025
|
|
5
|
45
|
2025
|
|
6
|
85
|
7225
|
|
7
|
55
|
3025
|
|
8
|
70
|
4900
|
|
9
|
60
|
3600
|
|
10
|
75
|
5625
|
|
Total
|
640
|
43350
|
Jika tabel di atas dituliskan dalam bentuk rumus, seperti ini jadinya:
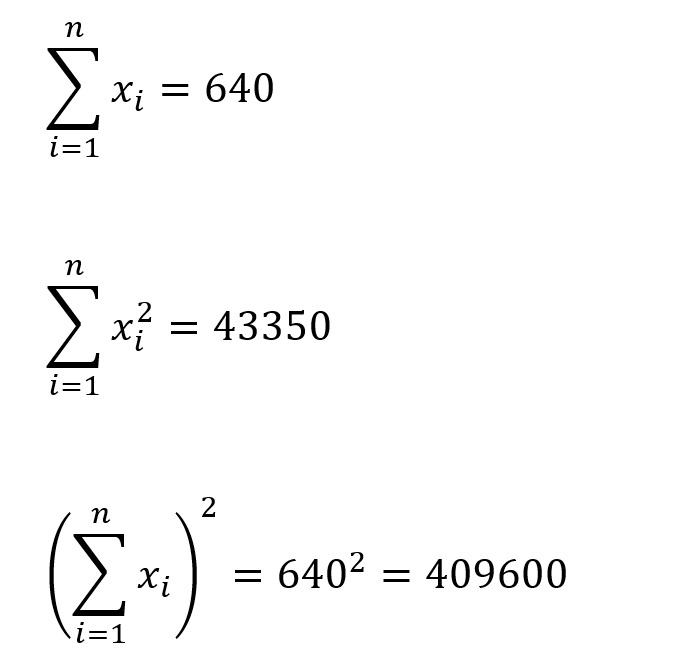
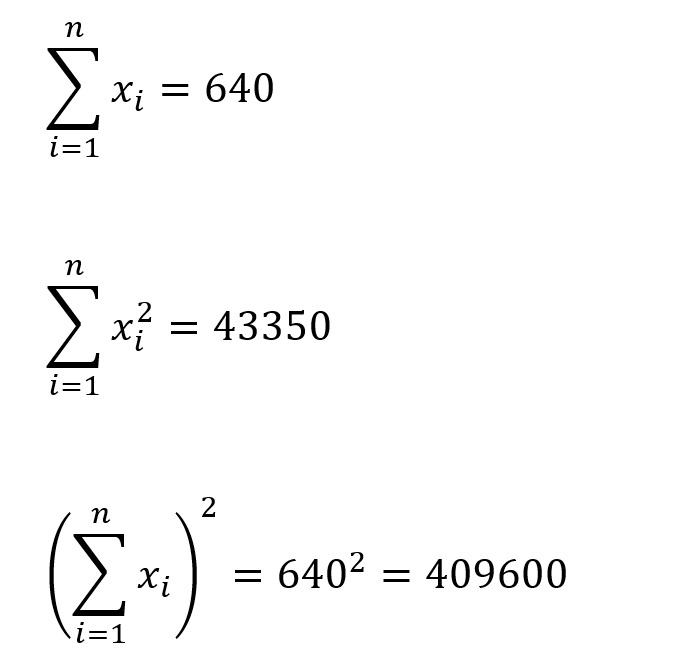
Dari perhitungan yang sudah diketahui dari rumus di atas, apabila angka dimasukkan ke dalam rumus varian. Maka menjadi sebagai berikut:


Sehingga kita mendapatkan nilai varian dari data tersebut yaitu 265,5.
Dari nilai varian di atas, kita juga dapat mencari nilai standar deviasi atau simpangan bakunya dengan cara sebagai berikut:
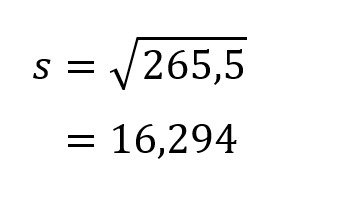
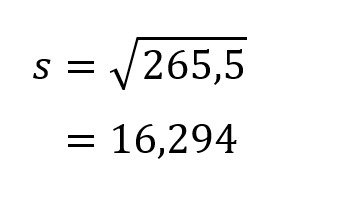
Nah, kita sudah mendapatkan standar deviasi dari kelompok A dengan pola belajar satu hari sedangkan kelompok B tiga hari.
Kelompok A memiliki standar deviasi 12,571, angka tersebut lebih kecil dibandingkan kelompok B yaitu 16,294. Tapi belum berhenti di sana. Bukan berarti memiliki standar deviasi tinggi membuktikan pola belajar 3 hari itu efektif. Karena jika dilihat kembali terdapat siswa dari kelompok B yang mendapat nilai di bawah 60 sebanyak 4 walaupun ada yang memiliki nilai tinggi yaitu 90. Sedangkan kelompok A yang mendapat nilai di bawah 60 hanya ada 2 orang walaupun nilai tertingginya hanya 80. Hal ini membuktikan bahwa standar deviasi tinggi belum tentu efektif. Sebaliknya, semakin kecil standar deviasi maka rentang datanya lebih kecil sehingga hasilnya lebih baik.
Dari contoh kasus di atas dengan waktu belajar yang lama ada kemungkinan murid tidak fokus belajar, lupa, dan faktor lainnya. Sedangkan yang belajar dalam waktu 1 hari bisa memaksimalkan waktunya dengan baik walaupun faktor lainnya juga bergantung pada kemampuan siswa itu sendiri

